• Number: Fractions
• Geometry: Angle, Shape, Symmetry
• Measurement: Area
Pattern Blocks appear to have been a part of a range of materials to come out of the Elementary Science Study in the late 1950s in The United States of America. Pattern Blocks are much more than simply a set of coloured blocks. They are a very powerful mathematics manipulative that may be used to support the teaching and learning of a variety of topics.

Pattern Blocks Videos

2:10 – Description of Pattern Blocks
4:00 – Activities
11:00 – Fractions
18:30 – Symmetry

Mathematical Language
Technically speaking, Pattern Block pieces are prisms, because they are three-dimensional and you can pick them up. The same is true of any block, When referring to Pattern Block pieces they are named according to the face.

The Yellow Hexagon is a regular hexagon, that is, all of the sides are the same length and all of the angles are the same size (congruent).

The best name for the orange piece is a square, however, it could be referred to as a quadrilateral, parallelogram, rhombus or rectangle as it meets the criteria for each of these four-sided shapes.

Likewise the green triangle is regular, that is all of the sides are the same length and the angles are congruent, so it is referred to as an equilateral triangle.

The red trapezium (trapezoid) – in fact it is an isosceles trapezium/ trapezoid.

The blue and tan rhombuses. Many young children refer to these pieces as
diamonds, but it would be better to use the mathematically correct name.
Using Pattern Blocks
Pattern Blocks are one of the most versatile mathematics manipulatives available. Young children begin by making pictures with Pattern Blocks and then progress to jigsaw type puzzles where Pattern Block pieces are placed inside an outline. While doing this, young children learn the names of the various pieces and have to rotate and flip pieces to fit into the puzzles.
An area relationship exists between most of the pieces and forms the basis for later fraction work.
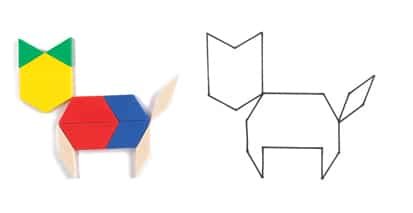
Transformations
As students complete puzzles with Pattern Blocks they will flip, slide and turn the various pieces. For example rotating a piece.

Symmetry
Students may determine the line and rotational symmetry of each Pattern Block piece. Later several pieces may be placed together to create shapes that have line and rotational symmetry.


Tessellation (Fitting Together Without Gaps)
A tessellation is made by fitting several of the same pieces together to cover a surface without any gaps or overlaps.


Measurement


Fraction Concepts
The area relationships illustrated here may be used to help students understand fraction concepts. For example one red trapezium covers half of the area of a yellow hexagon. A blue rhombus covers one-third of the area of a yellow hexagon and a green triangle covers one-sixth of the area of a yellow hexagon. Further fraction relationships between the blocks may be discovered. These relationships may be used to help students with other fraction concepts.

Typical Classroom Requirements
A class set:
A group of 4 students will require a set of 250 pieces. A class of 32 students would require 8 sets or 2000 pieces.
Note that Pattern Blocks are sold in different materials – plastic or wood and in different thicknesses – 5 mm and 10 mm. Be careful that when ordering extra sets to complement existing sets they match in terms of material and thickness.
Support and Complementary Materials
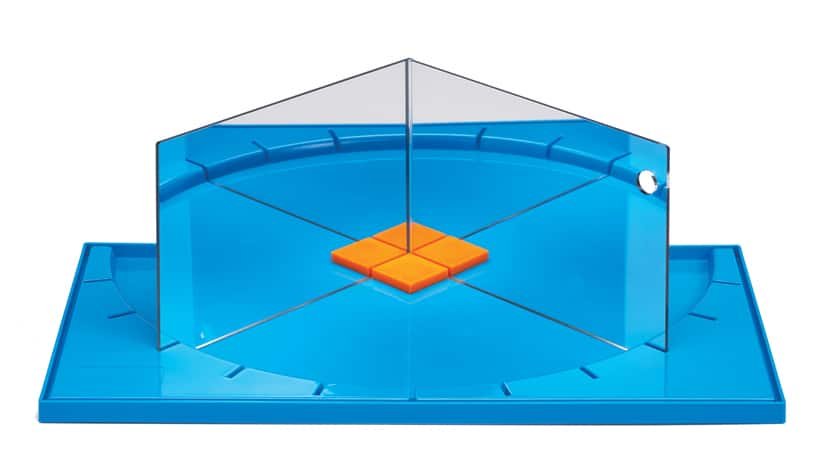
Geoland mirrors may be used to help teachers gain the most from a set of Pattern Blocks. A piece such as the orange square may be wedged into the corner of the hinged mirrors and the size of the angle determined with a little reasoning. The student will notice one original piece and 3 images, making a total of four pieces. The pieces can be seen to be arranged around a point. There are 360 degrees in a circle (or the total angle) so the angle must be 360 ÷ 4 or 90 degrees.

Pattern Block Activity Cards provide extra support to help teachers gain the most from the Pattern Block pieces. Initially, young children need to build shapes and copy shapes as they develop familiarity with the blocks. Later, activity cards may be used to introduce students to concepts such as symmetry.

