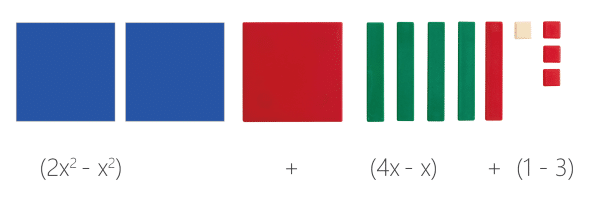• Number:
• Algebra: Equations, Equivalence
The Number Balance relies on the principle of equivalence. Weights are placed on either side of the fulcrum or pivot point. If a weight is placed on the peg marked 8 on the right arm of the balance then it may be ‘balanced’ by placing a weight on 6 and another on 2 on the left arm of the balance. The equation 8 = 6 + 2 is formed. Six may be balanced with 5 and 1, and by placing two weights on 3. This basic idea may be extended into early algebra.
Number Balance Videos
Mathematical Language
Balance, equivalent, fulcrum, pivot, weighs more, weighs less, weighs the same.
Using the Number Balance
The Number Balance may be used to learn about addition and particularly about the commutative property of addition, that is 6 = 4 + 2 and 2 + 4 = 6. Links to equations such as 2 + 2 + 1 + 1 = 4 + 2 may be made. The ideas of greater than and less than may be explained using a number balance. subtraction, multiplication and division may all be explored using a number balance. Later early algebra concepts may be introduced.
Greater than / less than
Subtraction
Multiplication
Division
Typical Classroom Requirements
A class set:
Support and Complementary Materials
