• Geometry: Shape - (Congruent, Similar,) Transformations - (Rotation, reflection, Translation,) Position, Angle
• Measurement: Perimeter, Area
• Algebra: Pattern
Geoboards were invented by Caleb Gattegno in the 1950s. Geoboards come in different sizes and configurations, but basically they all consist of a series of spaced pins. The spacing and the arrangement of pins may vary. For example, pins might be spaced at 10 mm or 20 mm intervals and are laid out in a square pattern. Other pins are laid out in an isometric grid, while still others are in a circular pattern. The most common Geoboard is set out in a square arrangement. Often a different arrangement will be featured on the back of the Geoboard. Plastic or elastic bands are placed around the pins on the Geoboard to form lines and shapes, making the Geoboard the ideal manipulative for developing geometry concepts.


Mathematical Language
Angle, area, congruency, patterns perimeter, position, reflection, rotation (turn). shape, similarity, symmetry, translation.
Using Geoboards
While using a geoboard a great deal of geometric language may be developed. For example, mathematical vocabulary such as intersect, perpendicular, right, acute, obtuse, as these naturally occur in the contexts of tasks and activities.
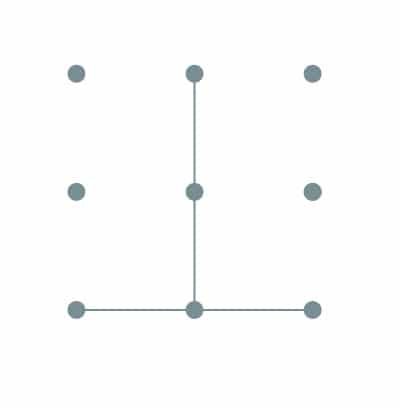
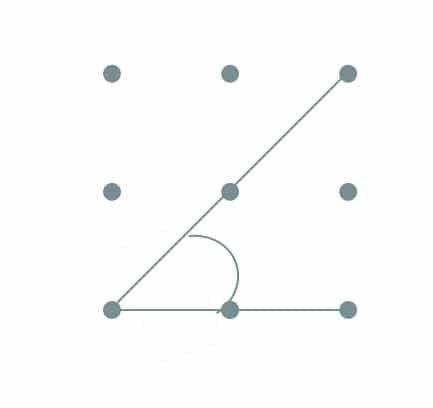
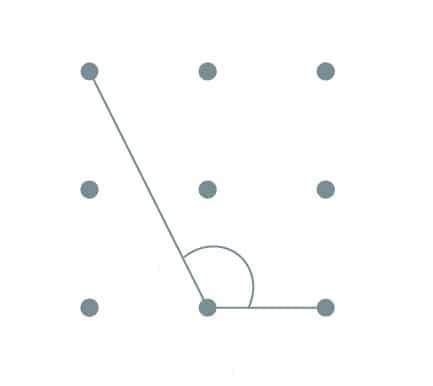
Triangles
Students will explore the properties of different 2D figures. Consider the language associated with triangles.
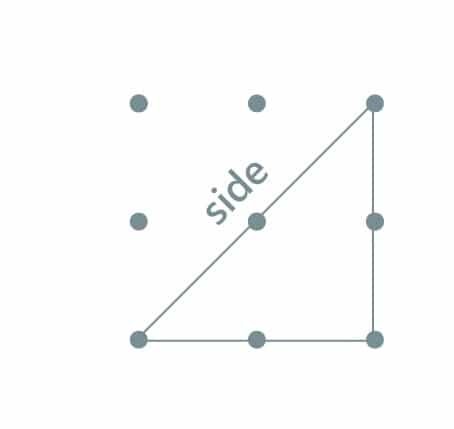
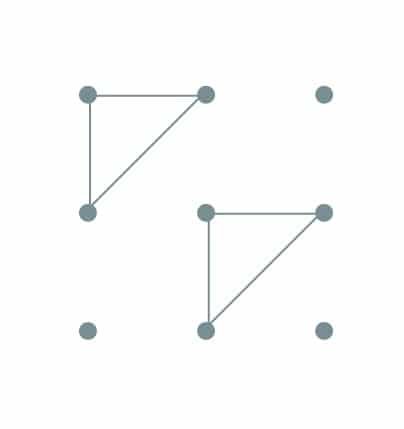
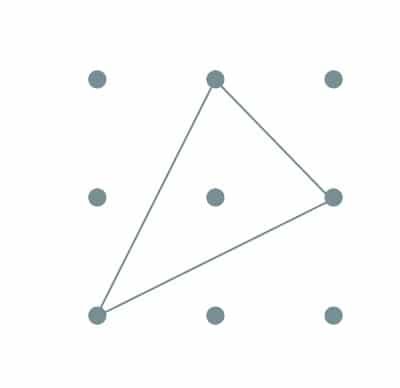
Similar triangles are the same shape. Corresponding angles are equal and corresponding sides are in proportion.
… and types of triangles.
Triangles may be named by their side lengths, angles or both.
Quadrilaterals
… and quadrilaterals.
… and polygons.

Perimeter / Area
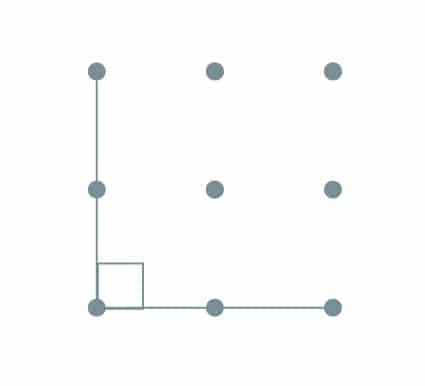
When first learning about perimeter and area it is simpler to create figures that do not have oblique lines. That is:
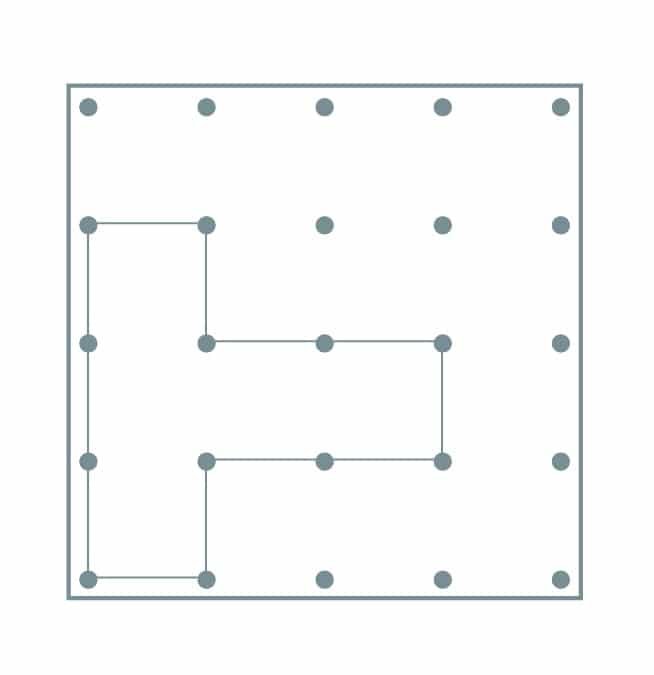
but not
Students can work out the perimeter of each figure they created by counting the segment between pins:
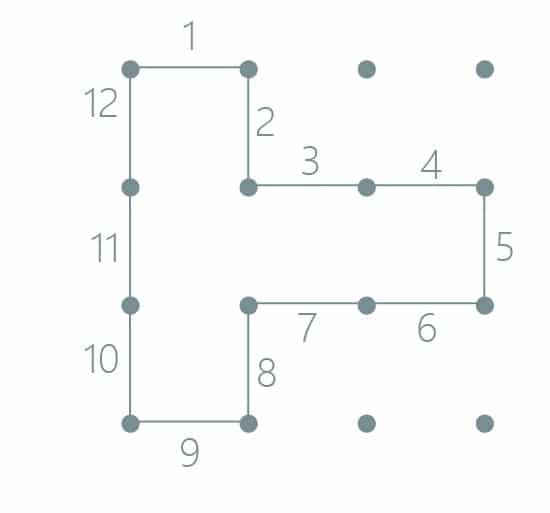
Keeping the line segments vertical or horizontal will make calculating perimeters much simpler. For example, this figure has a perimeter of 12 units.
Typical Classroom Requirements
An ample supply of bands of different lengths will be required if a variety of tasks are to be completed. If working in small groups, with students rotating through various task centres then four Geoboards would be sufficient.
A class set:
If students work in pairs, then 16 Geoboards would be sufficient to complete most tasks.
Support and Complementary Materials