Search
START TYPING AND PRESS ENTER TO SEARCH

• Precise Mathematical Language

• Higher Order Thinking

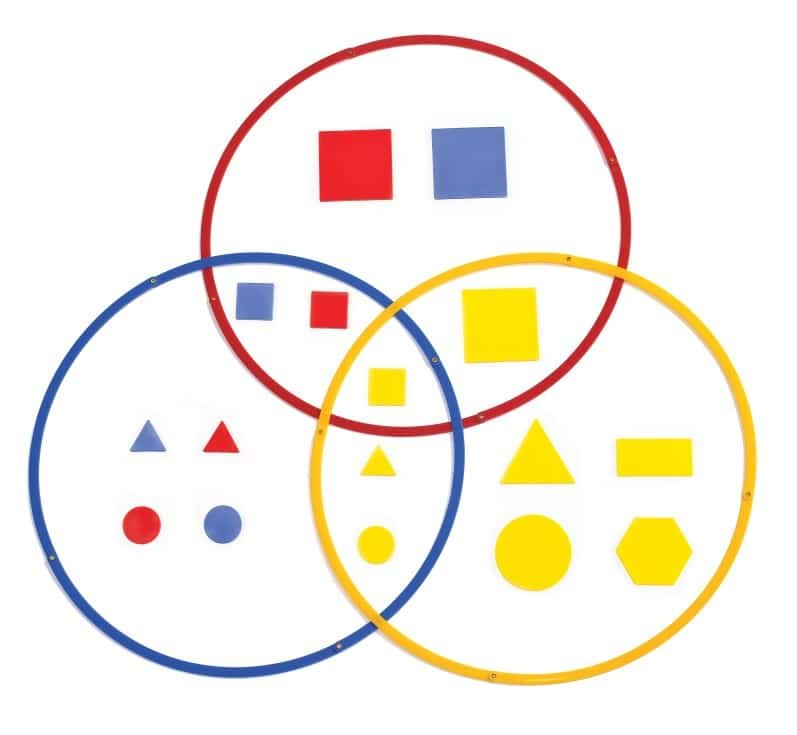
• Mathematical Reasoning: Logic, Venn Diagrams, Carroll Diagrams

It appears that William Hull (1968) and Zoltan Deines (1970) did much of the development work associated with Attribute Blocks or Logic Blocks as they once were called. They have strong links to the development of language and are often used as part of language related activities.

2 sizes, 2 thicknesses, 3 colours, 5 shapes

Videos

Mathematical Language

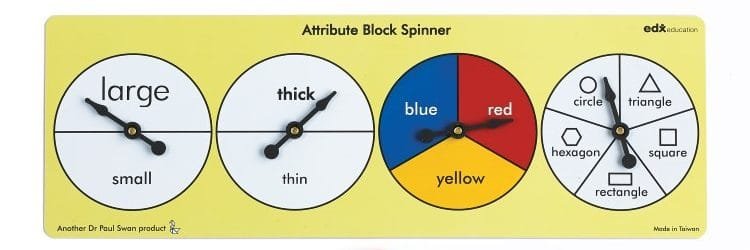
Attribute Blocks have four main attributes (hence the name).

• Size: large, small
• Thickness: thick, thin
• Colour: red, blue, yellow
• Shape: triangle, square, rectangle, circle , hexagon
• and, or & not (Boolean operators)

Using just four words, a person can describe any single piece in the set. For example, a small thin red rectangle describes a unique piece from the set. Some sets vary by eliminating one of the attributes. A typical set will contain 2 x 2 x 3 x 5 = 60 pieces.

Using Attribute Blocks

Attribute Blocks are the ideal piece of equipment for developing high order mathematical thinking logic and reason. For example, Venn Diagrams:

Attribute Blocks Article

Download Full Article

Typical Classroom Requirements

Attribute Blocks are often used in the early years of schooling, but rarely seen at higher levels. It is recommended that Attribute Blocks be used throughout the school as they can be used as the basis for some high level reasoning puzzles.

A class set:

– 6 Boxes for a class of 24, 8 for a class of 32 (one box between four students )

Support and Complementary Materials

There are clear links between the use of Attribute Blocks and the acquisition of precise mathematical language. Support materials such as the book Attribute Blocks: Developing Logic & Reasoning and the manual for Attribute Block Spinners highlight the language required to describe various blocks.

It is recommended that teachers be provided with support materials such as activity cards and possibly an Attribute Block manual in order to gain the most from this manipulative.

Relational Attribute Blocks

Essentially, these Attribute Blocks possess all of the characteristics of standard Attribute Blocks with one added feature – the small blocks are one-quarter of the size of the larger blocks. This means that some fraction relationships may be explored using these blocks.